コラム

1　ご挨拶

皆さん初めまして。日本情報システム株式会社ICTソリューション部の竹内です。
今年度入社し、取得知識のアウトプットを行うため、コラムを書くことになりました。
私のコラムは、「22卒が●●してみた」といったタイトルで公開していこうと思います。もっと専門的なコラムを期待している方は、２・３年後の私に期待をしてみてください。
少しでも皆さんに役立つ知識や、面白いと思っていただけるようなコラムを発信できるよう心掛けますので、どうか温か〜い目で見守って頂けると幸いです。

2　経緯

弊社のプロダクトやサービスは、お客様の大切な情報を保護することに重きを置いています。
OTP（One Time Password）¹やFIDO2(Fast IDentity Online 2)認証²を使って、お客様の大切な情報を保護しています。
弊社の業務に携わるうえで、これらの知識は必須でしたので、隙間時間を使って概要だけでも…と思い、調べ始めました。
そんな中、AWS（Amazon Web Service）から、フルマネージド量子コンピューティングサービス（Amazon Bracket³）が発表されました。AWSとは、米Amazon.com（, Inc.）が提供しているクラウドサービスです。クラウドサービスで量子コンピュータ⁴が使えるなんて便利な時代が来たものです。
もちろん、開発途中で実用できるものを提供しているにすぎませんが、量子コンピュータなんて22歳の私からしたら、ココロオドル文字列でしかありません。量子コンピュータのほうへ寄り道（さぼりではないです）していたら、どうやら量子コンピュータはRSA暗号（後述します）の解読が得意らしいとの記事を見つけました。弊社の商品においても、この話題は無視できないものです。ですので、私なりの考察を最初のコラムとして発信することにしました。
大前提として、2048bitのRSA暗号を解読できる量子コンピュータが普及するまで20〜30年（場合によってはそれ以上）かかるといわれています。まだしばらく先の話にはなりますが、来るべきその日に向けて思考を巡らせることは悪くないのではないでしょうか。
余談ですが、量子コンピュータはQuantum Computerと英訳されます。今後このキーワードを目にすることが増えると思うので、覚えておいて損はないでしょう。
前置きが長くなりましたが、本編へ行ってみましょう！！

3　そもそもRSA暗号って？

RSA暗号とは、公開鍵暗号方式で用いられるアルゴリズムです。
公開鍵暗号方式とは、暗号化に公開鍵を、復号に秘密鍵を用いる暗号化方式です。データの受信者が秘密鍵と公開鍵を作成します。秘密鍵はデータの受信者が誰にも知られないように保管し、公開鍵はデータの送信者に公開します。送信者は、受信者の公開鍵を用いてデータを暗号化します。暗号となったデータを復号できるのは、受信者の持つ秘密鍵だけなので、高セキュリティな通信が実現できます。また、公開鍵から秘密鍵を算出するには莫大な時間がかかります。そんな公開鍵暗号方式を実現するアルゴリズムの一つがRSA暗号です。この暗号を発明した三人（Rivest、Shamir、Adleman）の名前がRSAという暗号名の由来です。
現在使われている公開鍵暗号方式の中で、もっともポピュラーなアルゴリズムといっても過言ではないでしょう。安全性の根拠として、2048bitのRSA暗号では、現在最高性能のスーパーコンピュータを使っても解読に1億年以上かかるそうです。

RSA暗号では、2つの大きな素数を用いて鍵を作成します。
小さな素数を使って簡単な例をやってみましょう。

データの受信者側
① 素数p,qを用意する（例　p=23　q=37）
② 二つの素数をかけ合わせnを作る（n=p × q=851）
③ (p-1) × (q-1)を計算する（(23-1) × (37-1)=792）
④ (p-1) × (q-1)と互いに素（最大公約数が1）な自然数eを設定する（例　5）
⑤ e × d ÷(p-1) × (q-1)の余りが1になるようなdを設定する
（例　5 × 317 ÷792=2余り1　→　d=317）

受信者は上記の手順で秘密鍵を作成します。そのうち、nとeを公開鍵として送信者に渡します。送信者は公開鍵のnとeを用いて、送信したい内容を暗号化します。例えば送信したいデータとして33を考えてみましょう。

データの送信者側
① 送信したい内容x(x<n)を作成する（例　x=33）
② x^e÷nの余りをyとする（33⁵÷851=45987余り456　→　y=456）

こうしてできた暗号yを受信者に送信します。
受信者は送られてきた暗号yに対してnとdを使って復号をします。

データの受信者側
① y^d÷nの余りがx（456³¹⁷÷851=…余り33　→　x=33）

これで復号終了です。456³¹⁷は途方もない桁数になるので割愛させていただきます。
上記の結果通りになるか、是非皆さん自身でプログラムを組んでお確かめください。

RSA暗号は、秘密鍵なしでの解読に億年単位でかかるといわれています。その理由は、素因数分解の難しさにあります。
23×37は電卓を叩かなくとも、筆算で求めることができます。あるいは暗算で計算される方もいるかもしれません。851ですね。
しかし、851を素因数分解してみろといわれると簡単には求められません。これは素数が大きくなればなるほど難しくなります。こうなると総当たりで一つ一つ素数を当てはめてみるしかないのです。
これは古典コンピュータ（現在のコンピュータ）も同様です。私たち人間よりもはるかに計算速度は速いですが、やっていることは同じです。古典コンピュータも、高速で総当たりしています。私たち人間が予想できないくらい時間のかかる計算を、古典コンピュータが高速で行って億年程度まで短縮したにすぎません。ですので、RSA暗号は古典コンピュータにおいて安全であることが証明されています。

しかし、量子コンピュータは量子の「重ね合わせ⁵」という性質を利用し、一度に大量の処理を実行することができます。これにより、解読にかかる時間を大幅に削減できます。
これが、量子コンピュータがRSA暗号を解読できるようになると考えられている理由です。

4　考察してみた

22卒なりに考察してみました。

① 新しい暗号化方式が発明されるのではないか
② 量子コンピュータを導入できないと、セキュリティが大幅に低下してしまうのではないか
③ 現在の暗号化方式から移行する際のトラブルが多発するのではないか

それぞれについて、詳しく説明します。

4-1.　新しい暗号化方式が発明されるのではないか

新しいものが出たなら、対抗するのも新しいのが出てくるでしょ。といった発想です。
RSA暗号の鍵長（bit数）を長くすればいいとも思いましたが、これだと、鍵を作るのにも時間がかかってしまいます。
というのも、期待されている量子コンピュータでは、並列計算（同時に解をぶつける）は得意でも、単純な計算（一つ一つ計算する）では古典コンピュータと変わらないとされています。
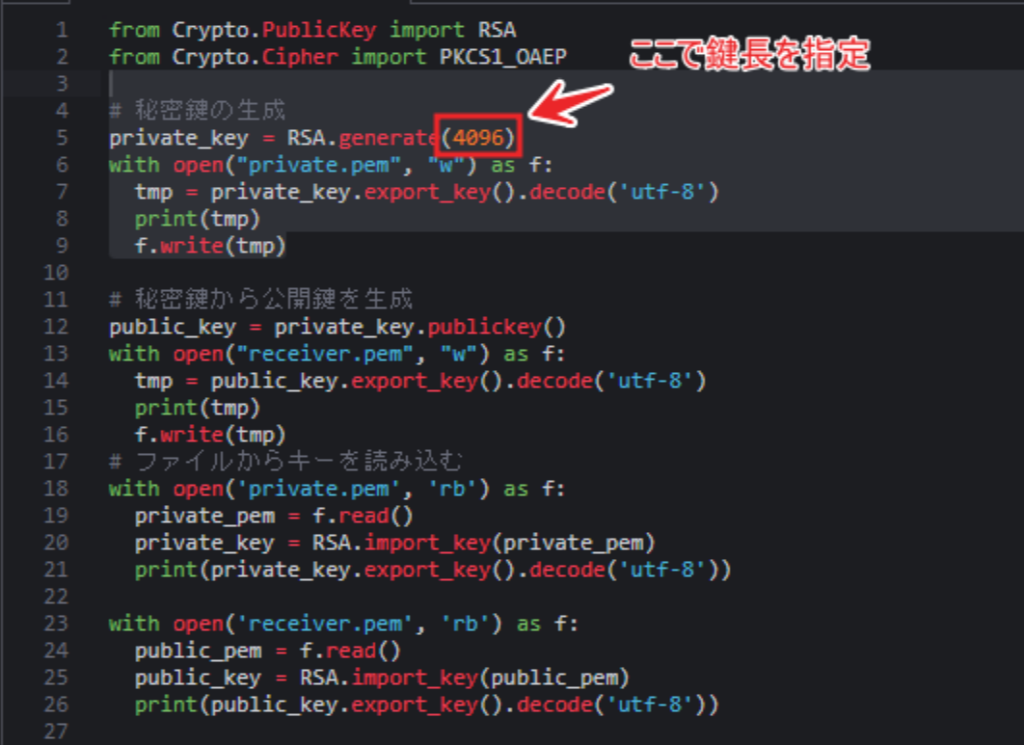
そこで、1024bit、2048bit、4096bit、8192bit、16384bitのRSA暗号を作成するPythonプログラムを作ってみました(実行環境：Cloud9　EC2　t2.micro)。

以下がサンプルプログラムです。
ライブラリがインストールされていない場合は、

pip install pycryptodome

を、実行環境のターミナルで実行してみてください。

結果は

1024bit →　0.74秒
2048bit →　1.41秒
4096bit →　6.56秒
8192bit →　32.86秒
16384bit →　1276.18秒

となりました。RSA暗号の作成 では、並列計算を用いていないので、量子コンピュータで作成しても、かかる時間は変わらないと予想されます。また、鍵長が長くなるとデータの送信や、復号に時間がかかってしまいます。
鍵が重複してしまうと、想定している送信先以外のユーザでも復号できるリスクが生じるため、鍵は各ユーザに対して一意でなければなりません。ユーザ一人一人に鍵の配布をしなければならないため、大規模な導入があった際に時間がかかりすぎてしまいます。

現在では、2048bitのRSA暗号が推奨されています。前述した通り、現在の最高性能のスーパーコンピュータでも解読に一億年以上の時間が必要だからです。1024bitでは、スーパーコンピュータで一年未満で解読できると予想されており、天と地ほどの差がありますね。
解読技術の発展により、今後推奨される鍵長が長くなるのは自明ですが、そこの分野が得意な量子コンピュータの発展からすればなんてことないでしょう。
作成する時間に対して、解読されてしまう時間が釣り合っていないと損をしますよね。商品化された場合は情報漏洩に直結します。
ですので、RSA暗号に代わる新しいものが出てくるんじゃないかと考えた次第です。

これについては、耐量子計算機暗号（量子コンピュータの解読に耐えうる暗号）の選定がもうすでに進められているようです。ベクトルという概念を用いた格子暗号や、符号理論に基づく符号ベース暗号等が有力視されています。
また、現在共通鍵暗号方式⁶で広く使用されているAES⁷（Advanced Encryption Standard）は、量子コンピュータの台頭において、鍵長を少なくとも2倍程度にすることで対策できるといわれています。

さらに、量子暗号と呼ばれる技術もあります。量子暗号は、共通鍵暗号方式に分類されます。量子コンピュータがどれだけ進化しようとも、現在では考えられないほど超高性能なコンピュータをもってしても、絶対に解読できないことが保証されている暗号です。この安全性は、「ワンタイムパッド」と「量子鍵配送」により、証明されています。
「ワンタイムパッド」とは、送受信するメッセージと同じ長さの乱数を事前に送信側と受信側で共有し、その乱数を暗号鍵としてメッセージの暗号化と復号を行うものです。暗号鍵は使用毎に破棄するため、使いまわしができず安全です。
「量子鍵配送」とは、「ワンタイムパッド」での鍵の共有を可能にする仕組みです。共有には、光子⁸を使用します。鍵の共有時に光子1粒ごとに1bitの情報を与え、送信者から受信者に鍵を送信します。もし途中で盗聴者に光子が盗まれてしまうと、その光子は受信者に届きません。一方で、盗聴者が盗み見て戻した場合、光子の量子力学的な性質により、光子の状態が変化してしまうため、盗聴の判別が可能です。光子の性質を用いて、盗聴の可能性がある暗号鍵は使用せず、安全な暗号鍵のみを共有することができます。
※参照：「光が導く次世代の暗号技術「量子暗号」」

実際の量子コンピュータがどのくらいの性能を持ち合わせるかによりますが、どの暗号を用いるか、さらなる考察が必要ですね。

4-2.　量子コンピュータを導入できないと、暗号化サービスの需要が低下してしまうのではないか

量子コンピュータが普及しても、金額や手間の関係で導入が遅れる方もいらっしゃるのではないかと予想しました。それに伴いデジタルディバイト（情報格差）のようなものが生まれ、何か不都合が出るんじゃないかなーと考えました。
量子コンピュータの普及後は、量子コンピュータと古典コンピュータを使い分けて利用するようになると考えられます。量子コンピュータを使う場面が限定的なことと、量子コンピュータを構成するために古典コンピュータを使用することが必要なので、両方のコンピュータが必要とされるはずです。
この使い分けには、暗号化サービスの使い分けもされるのではないかと考えました。古典コンピュータと量子コンピュータという二つの選択肢があることで、提供できる暗号化サービスの幅も広くなるはずです。選択肢があるということは、それだけ広い客層をターゲットにすることができるということです。
しかし、古典コンピュータのみの運用を続けると、提供できる暗号化サービスの選択肢も広がりません。選択肢がないということは、ターゲットがどんどん局所化してしまいます。
結果、古典コンピュータのみの暗号化サービスの需要が低下してしまうのではないかと考察しました。

4-3.　現在の暗号化方式から移行する際のトラブルが多発するのではないか

現在、RSA暗号を使った暗号化サービスは多いです。量子コンピュータによる解読に対抗して、暗号化サービスに耐量子計算機暗号を組み込むことが予想されます。
組み込むにあたって、耐量子計算機暗号に対する知識もそうですし、実現する技術力も必要になってきます。量子コンピュータの普及前から準備をしてきた企業さんは、なんてことないかと思います。
しかし、すべての企業さんが万全な準備をできるとは限りません。普及後から知識を蓄え、技術を育てるとなると、普及してから耐量子計算機暗号を導入するまで空白の期間ができてしまいます。そんなことになったら、暗号化サービスとしての価値が下がってしまうでしょう。問い合わせの温床になり、焦って開発もエラーを吐きまくってしまうかもしれません。私も開発者の端くれとして、こんな未来はまっぴらごめんです。

5　おわりに

皆さんいかがだったでしょうか。
私の考察ですが充分に可能性はあると思うので、将来に向けた知識の貯蓄が大切です。
2．経緯　で実現するまでに20〜30年（場合によってはそれ以上）かかると言われている。と述べました。しかし、AWSでのサービス提供開始や、今回のコラムを書いてみて、実現はもう少し早いんじゃないかなーという印象を受けました。
量子コンピュータの動向や、どんな耐量子計算機暗号があるかを知っておくだけでも、将来への貯蓄になります。今始めるのが一番早い！
このコラムを通して、皆さんも今後訪れるであろう量子コンピュータ時代の暗号課題を考察してみてはいかがでしょうか（私は楽しかったです）。

それでは皆さん、次のコラムでお会いしましょう！

¹  一度限り使用できる使い捨てのパスワードです。弊社ではAESを使用して発行しています。
² パスワードを使用しない認証方法です。サーバとクライアントの通信にRSA暗号を使用しています。
³ AWSで提供されているサービス名です。量子コンピューティングを提供しています。
⁴ 量子bitという単位で構成されているコンピュータです。古典コンピュータでは不可能な、並列計算が可能です。
⁵ 量子の「どちらに存在するか確定しない」という性質です。量子bitでは「0」「1」「0か1」の状態が存在します。
⁶ 共通鍵暗号方式とは、暗号化と復号に共通の鍵を使用する暗号方式です。秘密鍵暗号方式に比べ、暗号強度が落ちますが、処理が高速です。
⁷ 共通鍵暗号方式で用いられるアルゴリズムです。データを128bit毎に暗号化します。
⁸ 素粒子の一つであり、光の粒子です。なにかに触れると必ず状態が変化するという量子力学的な性質を持ちます。